2018江苏选调生行测数量关系备考:容斥问题
[导读] 2018江苏选调生考试备考攻略 招考公告 公示公告 课程体系 选调生QQ交流群51
| 2018江苏选调生考试备考攻略 | |||
| 招考公告 | 公示公告 | 课程体系 | 选调生QQ交流群518580884 |
| 笔试题库 | 笔试真题 | 咨询热线 | 咨询QQ | 咨询微信 | |
| 面试题库 | 面试真题 | ||
| 关注江苏国培教育微信公众号:(国培公考),免费咨询热线:4008015105随时随地掌握备考资讯! | |||
》》》 | 江苏选调生QQ在线咨询 | 江苏选调生微信在线咨询 | 《《《
选调生考试行测需要进行知识点完善,重点难点梳理。国培选调生网为帮助考生更好的备考行测考试,为大家整理了选调生行测指导之数学运算中的比例思想,助力考生顺利通过选调生考试。
容斥实际上就是一种计数原理,我们一般在计算总数时要先把所有的情况都相加,再把重复的情况排除掉(即把多次的变为一次)。在政法干警行测中我们常见的是两者容斥和三者容斥的问题。但是无论是解答两者容斥还是三者容斥问题,基本的方法有两招,一招就是文氏图,这也是我们常用的方法,另一招就是用公式。我们只有在解决极大值、极小值或者说最大值、最小值的问题上我们才会用公式,其他的题目一般就是画文氏图!下面我们来看看怎么用这两招解决容斥问题。
第一招:文氏图
我们从简单的两者容斥问题开始看看文氏图解题方法。
A.22人 B.24人 C.26人 D.28人
国培解析:总数50=20+12+既不近视又不超重的人-4,得出既不近视又不超重的人=22人。那么由此可知近视和超重的人一共是20+12-4=28人。
根据题目画出文氏图,如下图所示,总人数是50人,那么既不近视又不超重的人有50-28=22人。故答案选A。

下面再看看较为复杂的三者容斥问题。
例2.某调查公司对甲、乙、丙三部电影的收看情况向125人进行调查,有89人看过甲片,有47人看过乙片,有63人看过丙片,其中有24人三部电影全部看过,20人一部电影也没有看过,则只看过其中两部电影的人数是( )。
A.69人 B.65人 C.57人 D.46人
国培解析:根据题意画出文氏图,如下图所示。看过甲、乙、丙三部电影的人有:125-20=105人。那么只看过其中两部电影的人数是:(89+47+63)-2×24-105=46人。故答案选D。

通过上面两道题目我们可以体会到当题目中不涉及到最大值/最小值时,我们直接画文氏图就可以解决问题,利用文氏图解决问题的时候只要把全部的情况全部都算上,再把重复的变为单次就可以了!
第二招:公式
例3.在100个学生中,音乐爱好者有56人,体育爱好者有75人,那么既爱好音乐又爱好体育的人最少有多少人?最多有多少人?
既爱好音乐又爱好体育的人其实就是如下图中两个集合的交集,很容易看出当一个集合完全融于另一个集合时两个集合的交集最大。
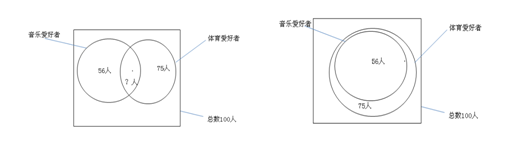
也就是说既爱好音乐又爱好体育的人最多有56人。两个集合分别用A、B表示。那么(A∩B)max =min {A,B}。同理三者容斥的最大值(A∩B∩C)max =min {A,B,C}。
既爱好音乐又爱好体育的人最少有多少人呢?我们知道:全集=爱好音乐+爱好体育-既爱好音乐又爱好体育+既不爱好音乐也不爱好体育,即I=A+B-A∩B +○,A∩B=A+B+○-I,A、B、I是固定不变的,那么求A∩B的最小值,那就要求○也最小,○最小可以为0。那么可知(A∩B)min=A+B-I,同理(A∩B∩C)min=A+B+C-2I,(A∩B∩C∩D)min=A+B+C+D-3I。
那么在本题目中既爱好音乐又爱好体育的人最少有:56+75-100=31人。
国培教育专家相信考生们通过上面的题目可以清晰地了解容斥问题的相关解决办法,熟练地掌握这两种办法尤其是文氏图法是很有必要的。希望各位考生体会方法,通过题目进行深化。
↓↓↓更多江苏省资讯欢迎订阅国培教育官方微信号:国培公考↓↓↓

- 上一篇:2018江苏省考公务员考试资料分析解题速度提升策略
- 下一篇:返回列表




